Visions of Oneness: Space-Time Geometry and Quantum Physics
Ignazio Licata et Teresa Iaria
Nr 01 . 9 janvier 2010
Table des matières
The two conceptual pillars of modern physics, General Relativity (GR) and Quantum Mechanics (QM), have very different structural characteristics and epistemological connotations. These differences directly influence the images and language we use for these two visions of the world, and it is from these that we wish to depart for a voyage through the most recent theoretical attempts at unification, with particular attention to the geometry of quantum potential and to pre-space structures. As Einstein wrote, “No physicist thinks with formulas,” and our intent is to gather the cognitive suggestions of contemporary art in order to propose new visions of the physical world.
1. Classic and Quantum, Global and Local
General Relativity (GR) may be considered the highest achievement of classical Physics, a formidable synthesis of the notions of space and time as a theatre of coordinates, of the description of the field of gravity, and of the equations of motion. Moreover, it has furnished the modern conceptual approach to studying the large-scale structure of space-time and the processes that take place in hyperdense matter (Hawking & Ellis, 1975). The essential form of the tensorial equations of Einsteinian gravity can be written as:
![]() (1)
(1)
With G being the Einstein tensor and T the stress-energy tensor.
[Figure 1]The peculiarity of eqs (1) leads to an effect of non-linearity – gravity gravitates! – which makes it very difficult to apply the traditional “local” processes of quantization to Einstein’s space-time curve. Moreover, a much more radical effect of non-locality is at the center of Quantum Mechanics (QM), the theory that threw many of the certainties of the classical image into crisis and that provided the tools for the investigation of Particle Physics and condensed matter.1
[Figure 2]In the EPR-Bell phenomena, in fact, objects separated in space and time show space-like correlations that are inexplicable with classical Physics, and that characterize the quantum statistics from which the most interesting properties of the structure of matter derive. Since the non-local correlations do not transport energy, they do not violate Relativity but nonetheless remain outside the bounds of the classical picture of the world. This situation goes under the name of “pacific coexistence” between Relativity and Quantum Physics (Shimony). The problem of reconciling the classical image of Einstein’s space-time and quantum non-locality is that of constructing a dynamic model of space-time in which the quantum processes also find a place, or that of developing a quantum geometrodynamics.
[Figure 3][Figure 4]2. Quantum Potential and Active Information
The most recent attempts at a geometric approach to quantum processes are owed to Wheeler2 based on Weyl’s geometry, and to Wood and Papini3 using a modification of the Weyl-Dirac theory. These theories have suggested that QM could be incorporated as a corresponding “deformation” of space-time. More recently Sidharth (Sidharth, 2002) has proposed a geometric interpretation of QM on the bases of noncommutative and non-integrable geometries. All of these attempts have an epistemological common denominator: the standard interpretation of QM. As Heisenberg observed at the dawning of quantum theory, Copenhagen’s interpretation is radically a-causal, and quantum processes cannot therefore be retraced to a space-time vision. This profoundly limits every attempt to understand Quantum Physics within the traditional Einsteinian space-time arena.
[Figure 5]In recent years interest in D. Bohm’s realist interpretation of QM has grown. Here let’s recall that Bohm’s interpretation reproduces all the results of QM without any ambiguity regarding the role of the observer.4 In this interpretation non-locality is not an “unexpected visitor,” as in the standard interpretation, but derives directly from quantum potential Q, a necessary term for the conservation of energy in Schrödinger’s equation:
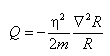 (2)
(2)
The form of potential (2) reveals some interesting properties: it depends on the amplitude R of the wave function and its action is like-space, exactly that called for in the EPR-Bell processes. Quantum potential contains global information of physical processes, defined as “active information,” or the contextual information of the system under observation and its environment, information that is not “external” to space-time but should rather be considered a type of geometric information “woven” into space-time itself. It is, further, a dynamic entity. Paraphrasing J.A.Wheeler’s famous saying about GR, we can say that the evolution of the state of a quantum system changes active global information, and this in turn influences the state of the quantum system, redesigning the non-local geometry of the universe.
3. Geometries of Non-Locality
The geometry subtending quantum potential has been explored by various authors.5 One very interesting result is that of Shojai & Shojai,6 who studied the behavior of particles at spin 0 in a space-time curve, demonstrating that quantum potential contributes to the curvature that is added to the classic one and that reveals profound and unexpected connections between gravity and quantum phenomena. All of this is expressed by a metric conformal such as:
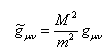 (3)
(3)
Where the expression for mass is : with Q as the quantum potential.
[Figure 6][Figure 7]This is a perfect image of quantum geometrodynamics that combines the gravitational and quantum aspects of matter, at least in terms of the level of macroscopic description of physical processes. In reality, once again, things are not so simple. Non-locality remains a phenomenon that rests uncomfortably with a “mechanical” vision of the universe, and it is not by chance that Bohm referred to QM and its interpretation as quantum non-mechanics, to reiterate that they could not be in any way understood as a return to the classical, but rather as the partial recovery of a “fuzzy realism.” Taking up the ideas of Heisenberg and G. Chew, the Birbeck group7 demonstrated that the entire symplectic non-commutative geometry identified by quantum potential can be derived from Weyl’s discrete algebra. In more directly physical terms, this means that there are two possible epistemological attitudes toward Eddington’s quantum sheet of geometrodynamics:
a) it is taken as primary but non-local, and therefore it is necessary to introduce additional hypotheses about its deep structure, or
b) the space-time manifold must be considered an emergence of the deepest processes situated at the level of quantum gravity.
Using the now famous image of complementarity in D. Bohm’s version, we can say that the entire connected and local structure of both space-time and the Shannon-Turing information we use to compute the events in it is the explicit order of a hidden, implicit order, which acts as a “fabric of reality” at a sub-quantum level, fundamentally discrete and non-commutative.8
4. The Quantum Foam of Implicit Order
The idea of a structure of relations subtending the observable forms of matter, energy and space-time was defined by J. A. Wheeler as “quantum foam,” with the precise intent of evoking the erosion of traditional notions toward the Planck scale typical of quantum gravity. Despite the ongoing lack of a strong unifying principle, the various versions of String theory have had a certain success in overcoming some of the impasses of Particle Physics, and it has been suggested that space-time manifold is the result of the interaction between p-branes, and that the acquisition of the masses in Higg’s Ocean finds its natural explanation in the mechanisms of uncurling and compactification.9 In reality, the majority of the versions of strings works, just like Quantum Field Theory, which is its closest relative, with a flat Minkowski space-time, while a correct, authentically relativistic (in the sense of GR) theory should be independent from the background, or not presuppose any metric signature. Various theories have these requirements. One is Penrose’s Twistor theory.10 To use Penrose’s own words, “a twistor is an object similar to the two-faced Janus, unitary but with one face turned toward QM and the other toward GR.” More precisely a twistor is and object without mass and charge and with spin, invariant for the conformal group, so as to find again the light-cone of Minkowski’s space-time. The famous representation by Robinson is based on a stereographic projection of Clifford’s algebra that defines the structure of twistors and allows the essential characteristics of the dynamic non-local “fragments” of space-time to be intuitively taken from it. Another very elegant theory that has the right relativistic requirements is Rovelli and Smolin’s “Loop quantum gravity”.11 The loops are closed field lines that do not depend on the coordinate system and therefore provide the basis for a relational description of space-time in the spirit of Leibniz. The theory presupposes a very particular space-time structure at the Planck scale: the operators associated with area and volume in fact have a discrete spectrum, giving birth to a complex and fascinating graph structure and thus furnishing a discrete combinatorial view of Physics.
5. Heraclitean and Parmenedian Aspects of Contemporary Physics
A rapid review of the relationships between the explicate order of space-time manifold and the theories that investigate the fine structure of quantum foam invites interesting reflection, both epistemological and cognitive.
[Figure 8][Figure 9]The entire history of Physics may be considered a progressive refinement of the models of space-time, from Newton’s absolute one to non-Euclidean and conformal geometries of the various classical and quantum geometrodynamics. All of these theories are characterized by the notion of “process,” understood as the evolution of a set of observables in space and in time. Quantum Physics has created an irreversible leak in the self-cohesion of such kind of view of the world, and the exploration of quantum gravity seems to propose the introduction of new geometric and algebraic structures that identify the weaving of relationships in the implicit order from which the very concepts of space, time, and evolution emerge. A unitary vision of the relationship between GR and QM will require, therefore, new conceptual terms to describe the deep complementarity between the Heraclitean and Parmenedian aspects of the physical world.
Bibliography
Bohm, D, Hiley, B. (1995), The Undivided Universe, Routledge
Brown, M. R. (2002), The quantum potential: the breakdown of classical symplectic symmetry and the energy of localisation and dispersion, http://arxiv.org/abs/quant-ph/9703007v3
Carroll, R. (2006), Fluctuation, Information, Gravity and the Quantum Potential, Springer
Hawking, S. Ellis,G. (1975), The Large Scale Structure of Space-Time, Cambridge Univ. Press
Hiley, B., Monk, N. A. M. (1998), A Unified Algebraic Approach to Quantum Theory, in Found. Phys. Lett., 11, 4, 371-377
Hughes, R. (1992), The Structure and Interpretation of Quantum Mechanics, Harvard Univ. Press
Huggett, S. A., Todd, K. P. (1994), An Introduction to Twistor Theory, Cambridge Univ. Press
Licata, I (2008), Emergence and Computation at the Edge of Classical and Quantum Systems, in
(Licata, I. & Sakaji, A. eds), Physics of Emergence and Organization, World Scientific, 2008
Randall, L., Sundrum, R. (1999), Large Mass Hierarchy from a Small Extra Dimension, in Physical Review Letters, 83, 17, 3370–3373.
Riotto, A (2000), D-branes, string cosmology, and large extra dimensions, in Phys. Rev. D 61, 123506
Rovelli, C. (2007), Quantum Gravity, Cambridge Univ. Press
Shojai, A., Shojai, F. (2004), Constraint algebra and equations of motion in the Bohmian interpretation of quantum gravity, in Class. Quantum Grav. 21 1-9
Sidharth, B. G. (2002), Geometry and Quantum Mechanics, http://arxiv.org/abs/physics/0211012
Wheeler, T. (1990), Quantum measurement and geometry, Phys. Rev. D 41, 431 – 441
Wood, W.R., Papini, G. (1995) ,A geometric approach to the quantum mechanics of de-Broglie–Bohm and Vigier”, in The present status of quantum theory of light, Proc. of Symposium in honor of J.P. Vigier, York University.
Citer cet article
Ignazio Licata et Teresa Iaria, « Visions of Oneness: Space-Time Geometry and Quantum Physics », [Plastik] : Être ici et là : La relativité générale et la physique quantique #01 [en ligne], mis en ligne le 9 janvier 2010, consulté le 03 juillet 2025. URL : https://plastik.univ-paris1.fr/2010/01/09/visions-of-onenness/ ISSN 2101-0323